The trapezoid volume formula utilizes the fact that while the bases are unequal trapezoids at parallel orientations, the height remains perpendicular.

By taking the average area of the two bases and multiplying by the height, you can calculate the overall volume.

Specifically, V = 1/2 x h x (B1 + B2), where B1 and B2 represent the lengths of the two parallel sides of each trapezoid base, and h equals the height or depth between the planes of the bases.

Though more intricate than basic box volume, this equation provides an accurate method for determining the quantity of space within a three-dimensional trapezoidal prism.

Finding the volume of three-dimensional geometric shapes is a fundamental mathematical skill.

When dealing with prisms – solids enclosed by two parallel and congruent polygonal bases joined by rectangular faces – the volume formula is simple: Base Area x Height.

However, things get more complicated when the bases are non-parallel trapezoids rather than rectangles or squares.

In these uniquely-shaped prismatic solids called trapezoidal prisms, a specialized formula is required to account for the irregular shape.

What is a Trapezoidal Prism?

A trapezoidal prism is a three-dimensional, straight-sided shape made up of trapezoids and rectangles.

One end of the shape consists of a trapezoid as the base, while the other end is a similar trapezoid at a parallel orientation as the top (so the sides are still parallel, even if the top and bottom widths are different).

The other faces along the length of the prism are rectangles.

Some key properties that identify trapezoidal prisms are:

• The bases on the top and bottom are parallel trapezoids (the sides are parallel to each other)
• The lateral faces down the sides of the prism are rectangles.
• There are six faces: two bases (top and bottom) and four side rectangles.
• They have right angles between all adjacent edges.

The non-parallel sides and angles of the trapezoids make finding the volume more challenging than a standard box shape. But using the trapezoidal prism formula helps simplify it.

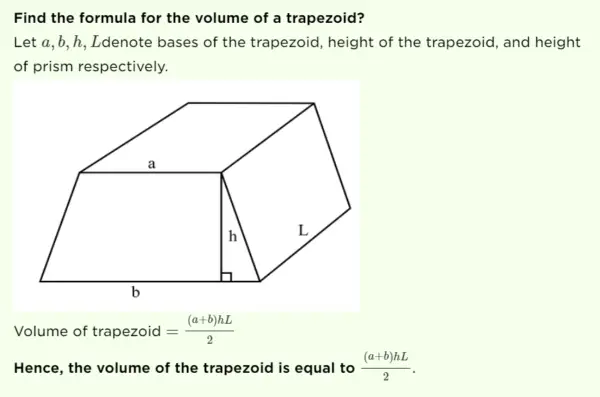
Trapezoid volume Formula

Since trapezoidal prisms have non-parallel bases, we can’t just multiply base area x height to find the volume. But we can still find the volume if we know:

• B1 and B2 = the two base lengths of each trapezoid (the parallel sides)
• b1 and b2 = the two non-parallel side lengths of each trapezoid
• h = the height between the two bases

The formula is:

V = 1/2 x h x (B1 + B2)

Where:

• V is the volume
• B1 and B2 are the lengths of the two parallel sides
• b1 and b2 are the non-parallel sides
• h is the height between the bases

This formula essentially takes the average of the areas of the two bases and multiplies it by the height, giving you the overall volume.

The work is in finding the base areas based on the side lengths.

But once you have the base areas, finding volume is no problem even without parallel sides

Examples Finding using Trapezoid Volume formula

Let’s walk through some examples of using the trapezoidal volume formula to find volumes, given different sets of parameters.

Example 1:

B1 = 12 cm
B2 = 16 cm
b1 = 10 cm
b2 = 14 cm
h = 8 cm

To find the volume using the formula:
V = 1/2 x h x (B1 + B2)

First find the two base areas, A1 and A2:
A1 = 1/2 x (b1 + B1) x h
= 1/2 x (10 cm + 12 cm) x 8 cm
= 1/2 x 22 cm x 8 cm
= 88 cm2

A2 = 1/2 x (b2 + B2) x h
= 1/2 x (14 cm + 16 cm) x 8 cm
= 1/2 x 30 cm x 8 cm
= 120 cm2

Now plug into the volume formula:
V = 1/2 x h x (B1 + B2)
= 1/2 x 8 cm x (12 cm + 16 cm)
= 1/2 x 8 cm x 28 cm
= 112 cm3

So the total volume of this trapezoidal prism is 112 cm3.

Example 2:

B1 = 5 in
B2 = 10 in
b1 = 4 in
b2 = 8 in
h = 12 in

Follow the same process to calculate A1, A2, and V:

A1 = 1/2 x (b1 + B1) x h
= 1/2 x (4 in + 5 in) x 12 in
= 1/2 x 9 in x 12 in
= 54 in2

A2 = 1/2 x (b2 + B2) x h
= 1/2 x (8 in + 10 in) x 12 in
= 1/2 x 18 in x 12 in
= 108 in2

V = 1/2 x h x (B1 + B2)
= 1/2 x 12 in x (5 in + 10 in)
= 1/2 x 12 in x 15 in
= 90 in3

The volume of this trapezoidal prism is 90 in3.

Real-World Applications

Architecture – Trapezoidal window bays on buildings form trapezoidal prisms. Architects need to calculate interior volumes when designing livable spaces and window placement.

Packaging – Some product containers and boxes are designed in a trapezoidal prism shape. Finding the volume helps determine how much the containers can actually hold.

Landscaping – Garden planter beds are sometimes built in trapezoid shapes using retaining wall blocks. Landscapers can use the volume formula to calculate how much soil or gravel to put inside.

Engineering – Beam supports under bridges or other structures often have a trapezoidal cross-section to save on materials. Engineers calculate strength capacities based on cross-sectional volumes.

Geometry – Textbook problems and standardized tests frequently ask students to calculate volumes of 3D shapes like trapezoidal prisms given a set of dimensions. The standard volume formula applies to any field working with geometric shapes.

Summary

Finding the volume of shapes with parallel bases is straightforward – just multiply base area by height.

Trapezoidal prisms throw in a curveball by having non-parallel trapezoid bases rather than basic rectangles.

But by taking the average base areas and factoring height, you can use the handy trapezoidal prism formula:

V = 1/2 x h x (B1 + B2)

Where B1 and B2 are the parallel side lengths, b1 and b2 are the non-parallel sides, and h is the perpendicular height between bases.

While it takes a few more calculations compared to basic boxes, this trapezoid volume formula makes solving easy.