Euler’s column buckling theory is a fundamental concept in structural engineering that explores the stability and load-bearing capacity of slender columns. Also known as column buckling, refers to the failure of a structural element subjected to high compressive forces.
Euler buckling is a fundamental concept in structural engineering, crucial for the design and analysis of slender columns under compression. Recognizing the mechanisms behind column buckling, knowing the Euler buckling formula, and mastering the factors that influence the critical buckling load are essential for anyone involved in civil, mechanical, or aerospace engineering.
This ratio compares the effective length of the column to its effective lateral dimension, like the radius of gyration. Slender columns with high slenderness ratios will tend to fail by buckling at lower loads than stockier columns.
The slenderness and resulting proneness to buckling failure depends significantly on the end conditions of the column and any lateral supports along its length.
Columns with pinned connections have a higher effective length factor and are more prone to buckling than columns with fixed end connections.

What Is Buckling? The Basics
Buckling refers to the sudden lateral deflection or bending of a structural element—most commonly, columns—when subjected to compressive forces.
Unlike material failure by yielding or crushing, buckling of columns often occurs at stress levels much lower than the material’s strength, suddenly and without warning.
The most notable demonstration of this is the failure of long, slender columns, which can deform dramatically at a specific load—the buckling load.
Euler Buckling Theory: The Foundation
The mathematical description of column buckling was formulated by the Swiss mathematician Leonhard Euler in the 18th century.
Euler’s buckling theory provides a powerful method to predict when a perfectly straight, slender column will become unstable and buckle when compressed.
Euler Buckling Formula and Equation
The Euler buckling formula (or Euler’s buckling formula) gives the critical buckling load at which a column will buckle:
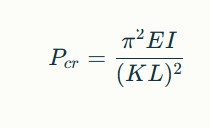
Where:
- Pcr: Euler’s critical buckling load (maximum axial force before buckling occurs)
- E: Young’s modulus (modulus of elasticity) of the column material
- I: Minimum second moment of area (moment of inertia) of the column cross-section
- K: Effective length factor, based on column end conditions
- L: Unsupported (actual) length of the column
This Euler buckling equation is sometimes written as the critical buckling load formula or the buckling load formula. It remains the bedrock for buckling equation calculations in engineering design.
Crippling load of a column
The critical load of a slender bar (columns) subjected to axial compression is that value of the axial load that is just sufficient to keep the bar a slightly deflected configuration.
- Case-I: P < Pcr Stable Equilibrium and No Buckling
- Case-II: P = Pcr Equilibrium State and Slight deflection
- Case-III: P > Pcr Unstable State and Buckling
When and Why Does Buckling Occur?
- Column buckling is most critical in long and slender columns, where bending deformations rapidly amplify once the critical load is exceeded.
- The buckling load is sensitive to the length and end-fixity of the column; longer columns with less lateral support buckle at lower loads.
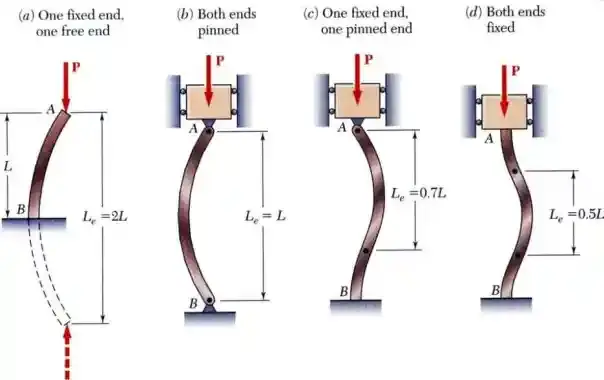
- For different end conditions, the effective length, KLKL, varies:
Assumptions of Euler Theory
- Cross-section of the column is uniform throughout its length.
- Column is initially perfectly straight and the load is applied axially.
- The column material is perfectly elastic , homogenous, isotropic and obeys hooke’s law.
- The length of the column is very high compared to its lateral dimension
- The column will fail only by buckling alone.
- All the direct stresses developed in the column are neglected.
- The self weight of the column is negligible.
In this theory the crippling load of the column changes with the change in actual length(l) of the column that depends on the end conditions of the column.
The term buckling means bending of the member to sideways showing a curved shape. This mode of failure is quick and hence dangerous.
Depending on slenderness ratio, columns are categorised as long and short columns.
A column is known as a long column if the length of the column compared to its lateral dimensions is larger. Such columns do not fail by crushing alone ,but also by buckling.
In case of long columns the direct compressive stress is negligible as compared to buckling stresses. Hence very long columns fail by buckling alone.
Application of Euler’s Buckling Formula
The euler buckling load formula is best for predicting the buckling of long, slender columns, like those found in bridges, towers, aircraft fuselages, and steel-frame buildings. For short, stocky columns with a low slenderness ratio, failure often occurs by crushing, and Euler’s formula for buckling does not apply.
Example: Calculating the Critical Buckling Load

Euler Column Theory
The unsupported length of the column can be calculated as below. The Euler column formula will give the susceptible to buckling. The loaded column and failure mode can be analyzed to know the column strength.
Source- A Textbook of Strength of Materials: (in S.I. Units) By R. K. Bansal
Real-World Importance: Preventing Structural Failure
Correctly estimating the critical buckling load ensures that buildings, bridges, and equipment stay safe under expected loads.
Failing to account for euler column buckling can lead to sudden, catastrophic collapses.
Modern design codes require engineers to check all compression members against buckling, often using the euler buckling theory as a starting point, then employing additional factors to account for imperfections and inelastic effects.
buckling of columns theory
Column buckling refers to the instability and failure of a slender, vertical structural member known as a column when it is subjected to compressive forces.
The column’s ability to support the load decreases with increase in the load applied on the column beyond the critical point.
At this load condition , the column experiences a sudden lateral deflection or bending, leading to a loss of stability and it may undergo a buckling phenomenon, which results in sudden and catastrophic failure.
Radius of gyration will give the equation for buckling theory. The differential equation can be solved to get a simple one.
Some time Buckling may occur even when the stresses developed are below that required for deformation of the member.
Further loading may cause significant and somewhat unpredictable deformations, possibly leading to complete loss of the member’s load-carrying capacity.
The buckling load of a column at which the column just buckles is called crippling load.
The critical load at which a column buckles depends on several factors, such as the length, cross-sectional area, material properties, and boundary conditions of the column.
The Euler formula is a widely used equation that relates these factors to the critical load.
In this blog post, we will explain the basics of column buckling and the Euler formula, and show some examples of how to apply them in engineering design.
We will also discuss some limitations and assumptions of the Euler formula, and how to account for them in practice.
Euler Buckling
Columns are the load carrying members designed to carry load from the slab to the footing. They should be well designed which helps in increasing the durability of the structure.
However due to several reasons they may be subjected to certain types of failures, which are to be eradicated in early stages to avoid unpredictable results.
In structural engineering buckling is a type of failure that is commonly observed in the long columns subjected to axial compression load.
The maximum load a column can withstand before buckling failure is called the critical buckling load. This load depends on the modulus of elasticity, area moment of inertia, and effective length of the column.
How to avoid buckling in columns is a crucial concern for structural engineers. One approach is to reduce the slenderness ratio of the column by increasing its cross-sectional area or reducing its length. Another method is to provide lateral support to the column, such as bracing or tie rods, which prevent lateral deflection and enhance its stability.
Euler derived a simple differential equation relating these parameters to predict the critical buckling stress and associated critical load.
If the applied load on a column exceeds this critical buckling load, the column can experience sudden excessive lateral deflection and buckling failure.
Therefore, engineers must design columns to have sufficient strength and stiffness to resist buckling. Three categories of columns are often considered: short columns that fail due to yielding, intermediate columns that fail by a combination of yielding and buckling, and long, slender columns that fail purely due to elastic buckling.
The key to preventing buckling failure is to ensure the compressive stress in a structural member under axial loads does not exceed the maximum usable stress.
This requires determining the critical buckling stress based on column dimensions, end conditions, and material yield strength. Then, applying appropriate safety factors to account for risks of buckling.
Consideration must also be given to higher order buckling modes beyond simple Euler buckling. Performing proper buckling analysis with accurate boundary conditions helps predict critical buckling loads and ensure adequate column design.
With sound engineering and awareness of parameters like slenderness ratio, effective length, and factor of safety against buckling, structural failures due to buckling can be avoided.
euler buckling load
Column buckling, also known as Euler buckling, refers to the sudden failure or deformation of a long, slender column under compressive loads. Several factors can contribute to column buckling, it is important to consider these factors during the design and analysis of columns to prevent buckling failures and ensure structural stability and safety.
Buckling analysis of Euler column is done to prevent failure. The stress in the column should not exceed the limits.
Following are some of the causes for column buckling
Compressive Load – Columns are designed to withstand compressive forces. If the applied load exceeds the column’s capacity, it can lead to buckling. Higher compressive loads increase the likelihood of buckling.
Slenderness Ratio – As the slenderness ratio increases, the column becomes more prone to lateral deflection and instability. Therefore, an increase in slenderness ratio results in buckling failure.
Column Material and Cross-Section – The material properties of the column, such as its modulus of elasticity and yield strength, play a crucial role in its resistance to buckling. Columns with higher stiffness and strength are less likely to buckle. Additionally, the shape and geometry of the column’s cross-section also affect its buckling behaviour. Columns with non-uniform or asymmetric cross-sections may exhibit different buckling characteristics.
Boundary Conditions – The manner in which a column is supported or restrained at its ends affects its buckling behaviour. Columns that are simply supported, i.e., free to rotate and displace laterally at their ends, are more prone to buckling compared to columns with fixed or clamped ends.
Imperfections and Initial Deflections – slight imperfections or initial deflections in a column can significantly influence its buckling behaviour. Small deviations from a perfectly straight shape can amplify under compressive loads and lead to buckling at lower loads than predicted by theoretical calculations.
Temperature Effects – . The thermal stresses can affect the buckling behaviour of the column, especially if the column is restrained or not uniformly heated or cooled.
To prevent column buckling, engineers employ various design strategies.
It includes increasing the column’s cross-sectional area, selecting materials with higher strength, and using bracing or reinforcement techniques.
Additionally, design codes and standards provide guidelines for determining the appropriate column dimensions and specifying acceptable slenderness ratios to mitigate the risk of buckling.
Effective Length Factor
The four different end conditions of the column taken into consideration here are
- One end is fixed and the other is free.
- Both ends of the column are in pinned condition.
- One end is fixed and the other end is in pinned condition.
- Both ends of the column are in fixed condition.
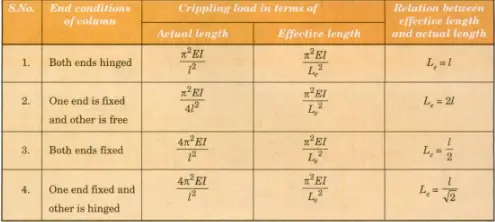
For each condition the actual length of the column (l) varies, therefore the crippling load formula in terms of actual length is different for different end conditions .
A relation is derived between the actual length(l) and effective length(L) of the column in different end conditions.
Frequently asked Questions (fAQ)
What are the different types of buckling?

The different types of buckling observed are Lateral Torsional buckling, Torsional Flexural Buckling, Global Buckling, Local buckling, Flexural Buckling.
What is effective length factor ?
The effective length factor K is the ratio between the effective length and original length. The Factor K depends upon the end/boundary Condition of the column.
What is the difference between buckling and yielding?
Buckling is a stability failure due to lateral deflection under compression.
Yielding is a material failure when stress exceeds the material’s yield strength.
In long slender columns, critical buckling load is usually lower than the yield load.
When do you use the Euler buckling formula?
For columns with a high slenderness ratio, where length greatly exceeds cross-section dimensions.
When the column is loaded axially and remains within the elastic region.
What is the role of the effective length factor K in the Euler buckling load formula?
K accounts for different end conditions; pinned, fixed, free, or combinations change the buckling behavior and thus the load required to cause buckling.
Euler’s column buckling theory gives engineers an idea about behavior of slender columns and helps in designing structures that can resist buckling under compressive loads. It serves as the basis for more advanced theories and design codes used in structural engineering today.
By applying Euler’s column buckling theory and implementing appropriate design techniques, engineers can effectively prevent buckling in columns, ensuring the safety and reliability of structures subjected to compressive loads.






