Euler Buckle Theory – Column Buckling And Equations

Euler’s column buckling theory is a fundamental concept in structural engineering that explores the stability and load-bearing capacity of slender columns. Also known as column buckling, refers to the failure of a structural element subjected to high compressive forces.

Column buckling a phenomenon that occurs when a slender column subjected to compressive loads undergoes lateral deflection, leading to a sudden loss of its load-carrying capacity.

The buckle formula, derived from Euler’s theory, determines the critical load at which a column buckles, taking into account factors such as the column’s length, cross-sectional area, and material properties.

This phenomenon was first studied in detail by Leonhard Euler. One of the key parameters that determines the critical buckling load for a column is the slenderness ratio.

This ratio compares the effective length of the column to its effective lateral dimension, like the radius of gyration. Slender columns with high slenderness ratios will tend to fail by buckling at lower loads than stockier columns.

The slenderness and resulting proneness to buckling failure depends significantly on the end conditions of the column and any lateral supports along its length.

Columns with pinned connections have a higher effective length factor and are more prone to buckling than columns with fixed end connections.

Column Buckling load Equation

To understand the behavior of columns under different loading conditions, engineers refer to the Euler curve for buckling.

This curve represents the relationship between the slenderness ratio of a column and its critical buckling load. The Euler stress formula is used to calculate the maximum compressive stress a column can withstand before buckling occurs.

Euler buckling occurs in long and slender columns with idealized boundary conditions. It is characterized by a uniform lateral deflection along the entire length of the column. 

The critical buckling load for Euler buckling is given by the Euler’s formula:

                                          Pcr = (π²EI)/ L^2

where:

• Pcr  is the critical buckling load
• E is the modulus of elasticity of the material
• I is the moment of inertia of the cross-sectional shape of the column
• L  is the effective length of the column, which depends on column  boundary conditions.

Crippling load of a column

The critical load of a slender bar (columns) subjected to axial compression is that value of the axial load that is just sufficient to keep the bar a slightly deflected configuration.

• Case-I: P < Pcr Stable Equilibrium and No Buckling
•  Case-II: P = Pcr Equilibrium State and Slight deflection
•  Case-III: P > Pcr Unstable State and Buckling

Assumptions of Euler Theory

1. Cross-section of the column is uniform throughout its length.
2. Column is initially perfectly straight and the load is applied axially.
3. The column  material is perfectly elastic , homogenous, isotropic and obeys hooke’s law.
4. The length of the column is very high compared to its lateral dimension
5. The column will fail only by buckling alone.
6. All the direct stresses developed in the column are neglected.
7. The self weight of the column is negligible.

In this theory the crippling load of the column changes with the change in actual length(l) of the column that depends on  the end conditions of the column.

The term buckling means bending of the member to sideways showing a  curved shape. This mode of failure is quick and hence dangerous. 

Depending on slenderness ratio, columns are categorised as long and short columns.

A column is known as a long column if the length of the column compared to its lateral dimensions  is larger. Such columns do not fail by crushing alone ,but also  by buckling. 

In case of long columns the direct compressive stress is negligible as compared to buckling stresses. Hence very long columns fail by buckling alone. 

Euler Column Theory

The unsupported length of the column can be calculated as below. The Euler column formula will give the susceptible to buckling. The loaded column and failure mode can be analyzed to know the column strength. 

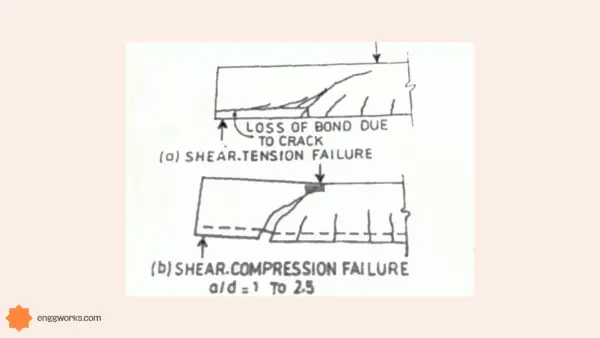
Source- A Textbook of Strength of Materials: (in S.I. Units) By R. K. Bansal

buckling of columns theory

Column buckling refers to the instability and failure of a slender, vertical structural member known as a column when it is subjected to compressive forces. 

The column’s ability to support the load decreases with increase in  the load applied on  the column beyond the critical point.

At this  load condition , the column experiences a sudden lateral deflection or bending, leading to a loss of stability and it may undergo a buckling phenomenon, which results in sudden and catastrophic failure.

Radius of gyration will give the equation for buckling theory. The differential equation can be solved to get a simple one. 

Some time Buckling may occur even when  the stresses developed are below that required for deformation of the member.

Further loading may cause significant and somewhat unpredictable deformations, possibly leading to complete loss of the member’s load-carrying capacity.

The buckling load of a column at which the column just buckles is called crippling load.

The critical load at which a column buckles depends on several factors, such as the length, cross-sectional area, material properties, and boundary conditions of the column.

The Euler formula is a widely used equation that relates these factors to the critical load.

In this blog post, we will explain the basics of column buckling and the Euler formula, and show some examples of how to apply them in engineering design.

We will also discuss some limitations and assumptions of the Euler formula, and how to account for them in practice.

Euler Buckling

Columns are the load carrying members designed to carry load from the slab to the footing. They should be well designed which helps in  increasing the durability of the structure.

However due to several reasons they may be subjected to certain types of failures, which are to be eradicated in early stages to avoid unpredictable results. 

In structural engineering buckling is a type of failure that is commonly observed in the long columns subjected to axial compression load.

The maximum load a column can withstand before buckling failure is called the critical buckling load. This load depends on the modulus of elasticity, area moment of inertia, and effective length of the column.

How to avoid buckling in columns is a crucial concern for structural engineers. One approach is to reduce the slenderness ratio of the column by increasing its cross-sectional area or reducing its length. Another method is to provide lateral support to the column, such as bracing or tie rods, which prevent lateral deflection and enhance its stability.

Euler derived a simple differential equation relating these parameters to predict the critical buckling stress and associated critical load.

If the applied load on a column exceeds this critical buckling load, the column can experience sudden excessive lateral deflection and buckling failure.

Therefore, engineers must design columns to have sufficient strength and stiffness to resist buckling. Three categories of columns are often considered: short columns that fail due to yielding, intermediate columns that fail by a combination of yielding and buckling, and long, slender columns that fail purely due to elastic buckling.

The key to preventing buckling failure is to ensure the compressive stress in a structural member under axial loads does not exceed the maximum usable stress.

This requires determining the critical buckling stress based on column dimensions, end conditions, and material yield strength. Then, applying appropriate safety factors to account for risks of buckling.

Consideration must also be given to higher order buckling modes beyond simple Euler buckling. Performing proper buckling analysis with accurate boundary conditions helps predict critical buckling loads and ensure adequate column design.

With sound engineering and awareness of parameters like slenderness ratio, effective length, and factor of safety against buckling, structural failures due to buckling can be avoided.

euler buckling load

Column buckling, also known as Euler buckling, refers to the sudden failure or deformation of a long, slender column under compressive loads. Several factors can contribute to column buckling, it is important to consider these factors during the design and analysis of columns to prevent buckling failures and ensure structural stability and safety. 

Buckling analysis of Euler column is done to prevent failure. The stress in the column should not exceed the limits. 

Following are some of  the causes for column buckling

Compressive Load –  Columns are designed to withstand compressive forces. If the applied load exceeds the column’s capacity, it can lead to buckling. Higher compressive loads increase the likelihood of buckling.

Slenderness Ratio  – As the slenderness ratio increases, the column becomes more prone to lateral deflection and instability. Therefore, an increase in slenderness ratio results in buckling failure.

Column Material and Cross-Section  – The material properties of the column, such as its modulus of elasticity and yield strength, play a crucial role in its resistance to buckling. Columns with higher stiffness and strength are less likely to buckle. Additionally, the shape and geometry of the column’s cross-section also affect its buckling behaviour. Columns with non-uniform or asymmetric cross-sections may exhibit different buckling characteristics.

Boundary Conditions – The manner in which a column is supported or restrained at its ends affects its buckling behaviour. Columns that are simply supported, i.e., free to rotate and displace laterally at their ends, are more prone to buckling compared to columns with fixed or clamped ends.

Imperfections and Initial Deflections –   slight imperfections or initial deflections in a column can significantly influence its buckling behaviour. Small deviations from a perfectly straight shape can amplify under compressive loads and lead to buckling at lower loads than predicted by theoretical calculations.

Temperature Effects – . The thermal stresses can affect the buckling behaviour of the column, especially if the column is restrained or not uniformly heated or cooled.

To prevent column buckling, engineers employ various design strategies.

It includes increasing the column’s cross-sectional area, selecting materials with higher strength, and using bracing or reinforcement techniques.

Additionally, design codes and standards provide guidelines for determining the appropriate column dimensions and specifying acceptable slenderness ratios to mitigate the risk of buckling.

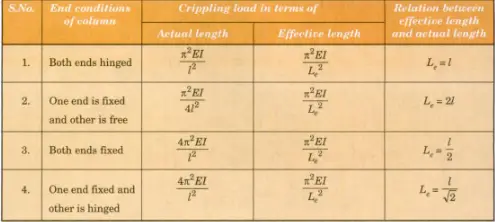
Effective Length Factor

The four different end conditions of the column taken into consideration here are

1. One end is fixed and the other is free.
2. Both ends of the column are in pinned condition.
3. One end is fixed and the other end is in pinned condition.
4. Both ends of the column are in fixed condition.

For each condition the actual length of the column (l) varies, therefore the crippling load formula in terms of actual length  is different for different end conditions .

A relation is derived between the actual length(l) and effective length(L) of the column in different end conditions. 

Frequently asked Questions (fAQ)

Euler’s column buckling theory gives engineers an idea about behavior of slender columns and helps in designing structures that can resist buckling under compressive loads. It serves as the basis for more advanced theories and design codes used in structural engineering today.

By applying Euler’s column buckling theory and implementing appropriate design techniques, engineers can effectively prevent buckling in columns, ensuring the safety and reliability of structures subjected to compressive loads.