Staircase Equation – also known as the Stairway Formula is an important underlying mathematical formula on which the most essential architectural features allowing circulation within multi-story buildings, staircases rely on .
At its core, the staircase equation establishes clear geometrical relationships between components like step depth, height, and number that impact aesthetics, functionality and safety.
Despite seeming trivial, miscalculating any variables in the equation leads to out of code, dangerous stairs in the real world.
Yet despite the simplicity of their function, staircases adhere to complex geometrical relationships and building code constraints.
This mathematical relationship governs the measurements between key components – the rise and run of each step, number of steps, total stair height, and overall length.
By inputting variables like desired stair pitch, run length, and total rise needed, the formula defines the permissible step dimensions and number of steps necessary for code-compliant staircase.
Beyond mathematical abstraction, the Staircase Equation has very practical implications in constructing a stair that is safe and functional for daily use.
Understanding and properly applying the formula when designing and building stairways is crucial for architects, builders, and do-it-yourselfers alike.
Miscalculation of stair dimensions and layout quickly leads to code violations, unusable stairs, injuries, and expensive reconstruction.
The key takes away – accurate use of the Staircase Equation is the foundation for transforming concept into reality for any well-designed stair.
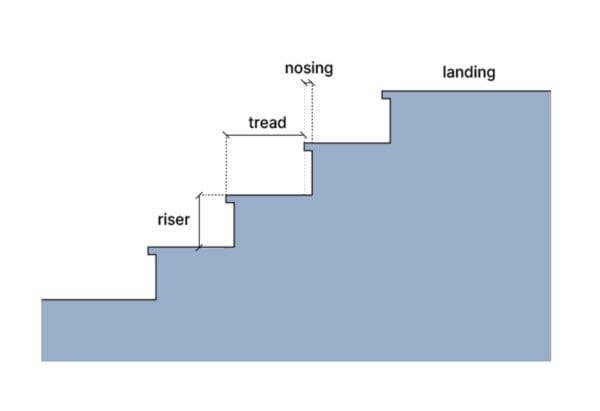
Defining Staircase Equation Variables
Let’s review the basic measurements involved in all staircases that the formula links together:
- Total Rise – The vertical height spanned from one floor to the next
- Run – Horizontal depth of each step
- Riser Height – The vertical face of each step you climb
- Number of Steps – How many steps total to connect the floors
- Stair Pitch – Angle of slope for the staircase, often 30-45°
The core staircase equation combines geometries of horizontal run length, vertical rise height and riser configurations to determine numbers of steps that fit code constraints and intended function whether in new construction or remodeling.
Classic Stairway Formula
The fundamental mathematical relationship governing all staircases is:
Total Rise (Height) = Number of Steps x Riser Height
OR written as:
Total Rise = Number of Steps x Riser
This elegantly simple equation underlies all staircase design once you plug in values. For a standard 10-foot room height being connected by a stair, you could have:
120 inches (10 ft) = 15 steps x 8-inch Risers
With just basic algebra, you can also reconfigure the formula to solve for any unknown:
Number of Steps = Total Rise ÷ Riser Height
There are more expanded versions of the stair equation, but this core relationship between the total rise in height, the number of steps, and the step dimensions sets fundamentals for calculations.
Building Code Constraints
However, not just any hypothetical stair dimensions derived are acceptable.
Residential and commercial building codes strictly govern geometry like tread depths and riser heights for safety and consistency.
Common convention is 7.5 to 9 inches for run length and 5 to 8 inches for riser height. This limits the slope and key dimensions so stairs aren’t dangerously steep or uneven.
Construction codes also mandate things like minimum head clearance, landing sizes, railings and lighting.
So the Staircase Formula gets further refined after establishing initial values to align with legal standards.
Adjusting Slope, Tread & Risers
The stairway equation can derive numerous combinations of steps that fulfill the change in height between floors.
This flexibility lets you tweak staircase slope and step proportions.
However, building codes fixed acceptable dimensions that dictate real world designs after initial mathematical relationships are established.
For example, an 11-foot room height could be spanned by 14 steps at a comfortable 7.25-inch riser height within code. Or 16 steps at a steeper 6.5-inch rise.
The former creates a more gradual staircase preferred in homes, while the latter fits tighter spaces.
Optimizing these real-world constraints and personal tastes is where staircase design progresses after the initial math.
Double Check All Stair Calculations
It can’t be overstated how imperative double-checking all figured dimensions is, both initially and against building codes.
A single mis-measured riser compromises stair safety and compliance. Identical step rise/run pairs MUST be used for proper function and safety.
Luckily, the repetitive geometry of stairs makes it simple to validate calculations and spot errors.
Consistently applying the stair formula principles protects against missteps in planning.
Putting Equation into Practice
Let’s walk through an example design scenario to connect a 12 foot ceiling between floors with a stairwell spanning 115 inches total rise.
We want gently sloped steps suitable for family use.
Starting with ideal run length dimensions and checking against code constraints yields an executable staircase plan:
- Use 9 inch step runs to ease climbing slope
- Set riser height at 7 inches based on building codes and desired pitch
- Plug into formula: Total Rise = Number of Steps x Riser Height
- 115 inches = Number of Steps x 7 inches
- 115 inches/7 inches = 16.4 steps
- Round to whole number = 16 steps
- Double check: 16 steps x 7 inch rise per step = 112 inch total rise
- Account for 3 inches of leftover height to finish top and bottom step integration.
This example workflow demonstrates applying the staircase formula to properly specify and calculate ideal rise-run step dimensions tailored to your stair project constraints.
Conclusion
The mathematical staircase equation certainly isn’t the most glamorous facet of architecture.
Yet modest math paved the way for staircases transcending ancient ziggurats to sleek modern high-rises.
This engineering equation remains timeless.
By meshing simple geometry with building constraints and site goals through basic algebra principles you unleash creative freedom for any stairwell.
The Staircase Formula foundations empower designing striking yet functional stairs from imaginations to reality.