Elasticity is a key mechanical property that all civil engineers must understand.
Elasticity, ability of a deformed material body to return to its original shape and size when the forces causing the deformation are removed. A body with this ability is said to behave (or respond) elastically.
When external forces are applied to a material or body, it undergoes some deformation. Up to a certain stress limit, this deformation may be elastic.
This means that when the external forces are removed, the material goes back to its original shape.
Beyond this elastic limit, permanent or plastic deformation can occur.
Understanding the nature of elastic forces and material elasticity is crucial for civil engineering design and analysis.
Hooke’s Law and Elasticity
Robert Hooke first defined the principle that strain in a solid is proportional to the applied stress within the elastic limit in 1660.
This relationship is now termed as Hooke’s law. It states that:
Force = Displacement x Spring Constant
Or
Stress = Strain x Elastic Modulus
This linear elastic behavior is key to quantifying elasticity. The slope of this linear region defines the elastic modulus or stiffness of the material.
Elastic Potential Energy Formula
Elastic potential energy is the energy stored in a body or material as work is done to deform it within the elastic limit.
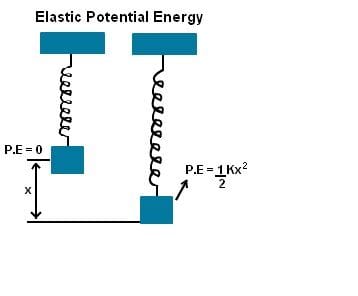
It can be calculated by:
U = 1⁄2 kx2
Where,
U = Elastic potential energy
k = Spring constant
x = Displacement
This energy is released upon the elastic body returning to its original shape.
Stress-Strain Curve Explained
The stress-strain curve graphs the relationship between stress (force per unit area) and strain (proportional deformation) for a material in a structural member undergoing tension or compression.
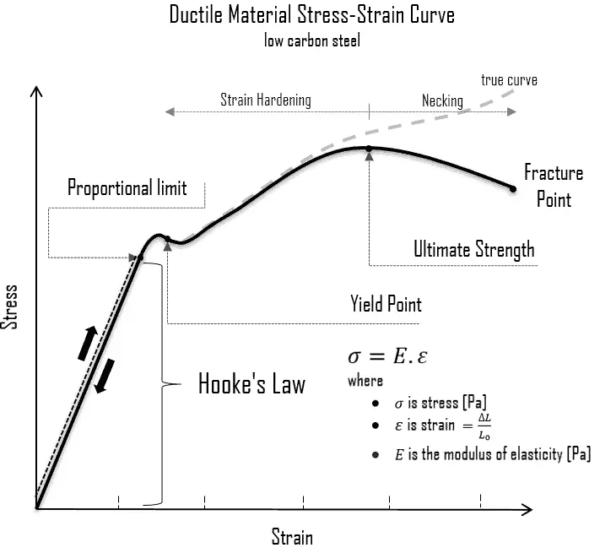
The initial linear region follows Hooke’s law. The slope is the elastic modulus.
At the proportional limit stress value, deviation from linearity occurs. The elastic limit is when deformation stops being fully recoverable.
Plastic deformation marks permanent strain beyond the ultimate stress point.
Stress-strain curves allow determining elastic ranges for design.
Modulus of Elasticity Examples
The modulus of elasticity (E) or Young’s modulus quantifies material stiffness. Some common examples include:
- Structural steel: 200 GPa
- Concrete: 20 to 40 GPa
- Wood (along grain): 10 to 15 GPa
- Rubber: 0.01 to 0.1 GPa
Higher modulus means the material is stiffer, requiring more load to deform by a given amount according to Hooke’s law.
Elasticity in Materials Science
Materials science examines how complex microstructural factors affect macro-scale elastic properties.
This includes considering how:
- Crystal structure arrangements affect atomic bond elasticity
- Defects like vacancies influence elastic response
- Grain boundaries impact deformation
- Cooling rate and heat treatment alter modulus values
Inducing controlled elastic behavior requires understanding how processing influences structure and properties.
Elastic and Inelastic Deformation
Elastic deformation involves reversible stretching or compressing of atomic bonds when a low stress is applied.
The material returns to its resting shape after removing the load as no permanent changes occur in the microstructure.
Inelastic deformation can involve irreversible atomic displacements from the starting positions.
This permanent strain remains after removing the stress. Examples include plasticity and creep.
Careful design is required to keep maximum service stresses low enough to prevent inelastic deformation.

Elasticity Physics Problems and Solutions
Physics problems provide simplified scenarios to apply elastic concepts and equations for various geometries and loading cases.
Example cases could analyze:
- The deflection of beams under bending forces
- Stretching of tie rods under axial tensile loads
- Compression of concrete columns
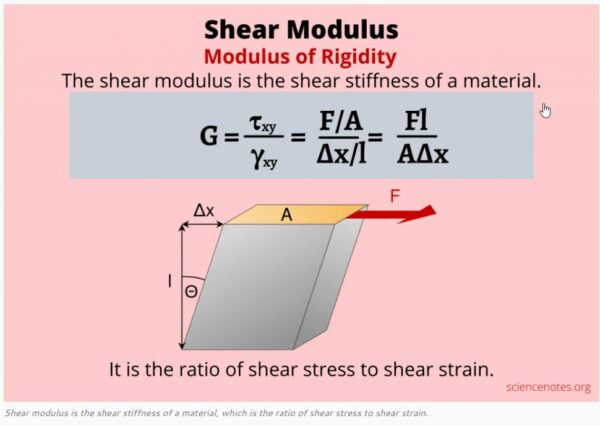
- Shear deformation in bolted joints
Analyzing such physics problems builds intuition and showcases quantitative applications of elasticity.
Elastic Collision Equations
Perfectly elastic collisions involve objects bouncing off each other without loss of kinetic energy.
The initial and final velocities can be calculated by conservation of momentum and energy considerations providing the coefficient of restitution is known.
Studying elastic collision scenarios helps further understand elastic reactions.
Elasticity of Metals, Polymers, Ceramics
Elastic modulus values vary substantially across metals, polymers, and ceramics based on atomic structure.
Metals demonstrate high but variable elasticity and plasticity with ductile failure.
Atomic bonds stretch under tensile loads and reform after load removal.
Polymers like rubber exhibit near elastic behavior even to over 100% strain.
Molecular chains uncoil then recoil elastically.
Ceramics are brittle with low failure strains. Ionic/covalent bonds allow small elastic deformation ranges before fracture.
Elasticity and Young’s Modulus Relationship
Young’s modulus E is the most common metric used to represent elasticity.
It links elastic stress to strain in the linear region per Hooke’s law.
Higher modulus values indicate greater material stiffness and resistance to elastic deformation when a force is applied compared to soft materials.
Optimizing elasticity requires selecting materials with appropriate moduli for the design application.
Hopefully this overview provides a foundational understanding of key concepts related to elastic forces and elasticity from a civil engineering perspective