How to Calculate Stress in Cantilever Beams for Different Loading Conditions

Engineers must understand and accurately determine the stresses in cantilever beam designs to create safe, optimized structures.

Cantilever beams experience various stresses including bending stress, shear stress, and deflection stress.

Carefully analyzing these stresses using calculations, formulas, and analysis techniques allows the maximum load capacity to be determined.

Calculating Stress in Cantilever Beams with point load

point loads are common for cantilever structures such as balconies and signs.

stress in Cantilever Beam Formulas – The primary formula for calculating stress in a cantilever beam is:

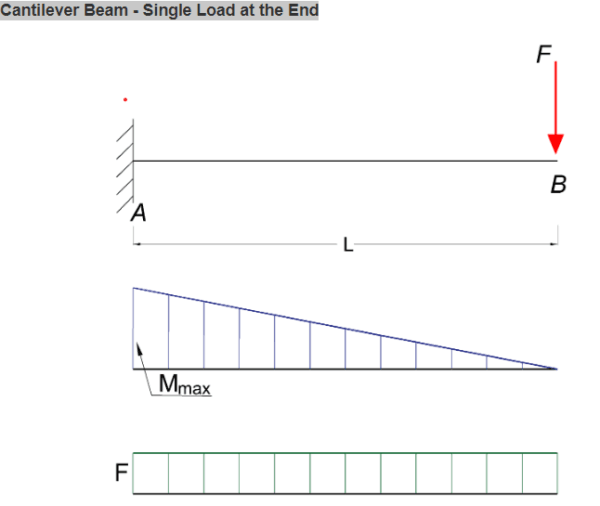
Maximum Reaction Force

at the fixed end can be expressed as:

R_A = F                              (1a)

where

R_A = reaction force in A (N, lb)

F = single acting force in B (N, lb)

Maximum Moment

at the fixed end can be expressed as

M_max = M_A

          = – F L                               (1b)

where

M_A = maximum moment in A (Nm, Nmm, lb in)

L = length of beam (m, mm, in)

This is the fundamental flexural stress formula used to determine the bending stress from applied loads at any point on a cantilever beam based on beam geometry and material properties.

This formula assumes an elastic, linearly elastic isotropic material. Stresses may exceed yield strength and the beam may experience some plastic deformation.

Some key notes when using this equation:

• It gives stress due to BENDING ONLY, not including shear stress or deflection stress.
• Parameters must be consistent (N vs lb, m vs in)

So in summary, the foundation of cantilever beam stress analysis is this flexural stress formula from applied loads.

Cantilever Beam Stress Calculations

By using the cantilever beam stress formulas, calculations can be performed to find stresses at any point. Key calculations include determining…

Stress

The stress in a bending beam can be expressed as

σ = y M / I                                     (1d)            

where

σ = stress (Pa (N/m²), N/mm², psi)

y = distance to point from neutral axis (m, mm, in)

M = bending moment (Nm, lb in)

I = moment of Inertia (m⁴, mm⁴, in⁴)

Deflection Stress Factors

In additional to tensile and compressive stresses, deflection stress plays a key role in cantilever design. Deflection stress is calculated by…

Maximum Deflection

at the end of the cantilever beam can be expressed as

δ_B = F L³ / (3 E I)                                      (1c)

where

δ_B = maximum deflection in B (m, mm, in)

E = elastic modulus (N/m² (Pa), N/mm², lb/in² (psi))

I = moment of inertia (m⁴, mm⁴, in⁴)

b = length between B and C (m, mm, in)

Maximum Stress in Cantilever Beams

Maximum stresses establish the load capacity limits for cantilever beams. For safe design, the maximum stresses should not exceed…

The maximum moment in a cantilever beam is at the fixed point and the maximum stress can be calculated by combining 1b and 1d to

σ_max = y_max F L / I   

Stresses in Cantilever Beams with UDL

Cantilever beams often support uniformly distributed loads (UDL) in structural design cases. The stresses in a cantilever with UDL…

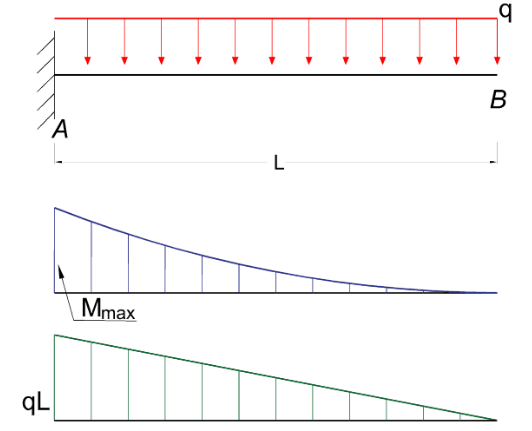
Maximum Reaction

at the fixed end can be expressed as:

R_A = q L                                (3a)

where

R_A = reaction force in A (N, lb)

q = uniform distributed load (N/m, N/mm, lb/in)

L = length of cantilever beam (m, mm, in)

Maximum Moment

at the fixed end can be expressed as

M_A = – q L² / 2                             

Maximum Deflection

at the end can be expressed as

δ_B = q L⁴ / (8 E I)                              

where

δ_B = maximum deflection in B (m, mm, in)

q – Uniform load (N/m, N/mm, lb/in)

 L – Length of beam (m, mm, in)

 I – Moment of Inertia (m⁴, mm⁴, in⁴)

 E – Modulus of Elasticity (Pa, N/mm², psi)

 y – Distance from neutral axis (m, mm, in)

Cantilever Beam – Declining Distributed Load

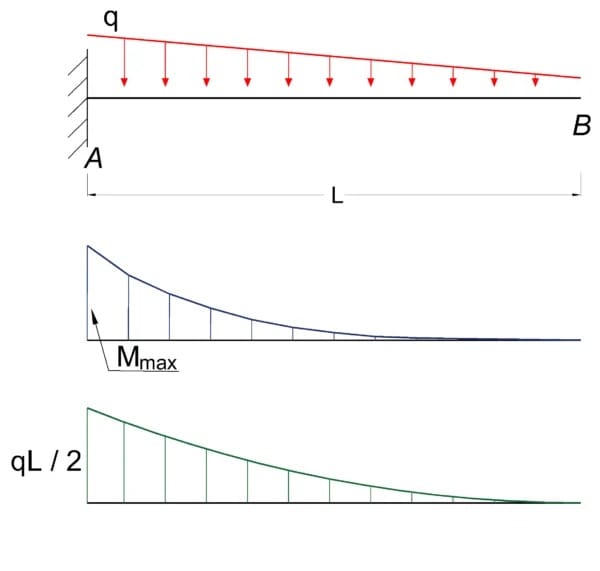
Maximum Reaction Force

at the fixed end can be expressed as:

R_A = q L / 2                              (4a)

where

R_A = reaction force in A (N, lb)

q = declining distributed load – max value at A – zero at B (N/m, lb/ft)

Maximum Moment

at the fixed end can be expressed as

M_max = M_A

          = – q L² / 6                           

where

M_A = maximum moment in A (N.m, N.mm, lb.in)

L = length of beam (m, mm, in)

Maximum Deflection

at the end of the cantilever beam can be expressed as

δ_B = q L⁴ / (30 E I)                                  

where

δ_B = maximum deflection in B (m, mm, in)

E = modulus of elasticity N/m² (Pa), N/mm², lb/in² (psi))

I = moment of inertia (m⁴, mm⁴, in⁴)

Conclusion

Properly determining and analyzing the stresses in cantilever beams provides the necessary insight into beam capacities and failure modes.

By following the best practices highlighted, civil engineers can efficiently design safe, optimal cantilever beams for infrastructure and construction projects.

The key considerations include accurately calculating stresses using the correct formulas, analyzing deflection and stress distribution, checking for maximum allowable stresses, and performing analysis for combined or concentrated point loading scenarios.

This comprehensive stress analysis ensures cantilever beam designs minimize cost and safety risk.