Concrete is one of the most widely used construction materials in the world. Its popularity stems from its high compressive strength, durability, and versatility. However, concrete is a complex composite material whose properties depend on its composition and structure. One of the most important properties of concrete is its modulus of elasticity. This post will provide a comprehensive overview of the modulus of elasticity of concrete.
What is Modulus of Elasticity?
The modulus of elasticity (also known as Young’s modulus) is a measure of the stiffness of a material. It is defined as the ratio of the stress applied to the material to the resulting strain. In simple terms, it describes how much a material will deform under a given amount of stress. A high modulus of elasticity indicates that the material is very stiff, while a low value suggests a more flexible material.
For concrete, the modulus of elasticity is a key parameter that influences the load-carrying capacity of concrete structures. It is a factor in computing the stresses and deformations in concrete members subjected to loads. The modulus of elasticity is also used to predict the flexural stiffness and deflections of concrete beams and slabs.
Factors Affecting Modulus of Elasticity of Concrete
The modulus of elasticity of concrete depends on a number of factors related to the composition, curing conditions, and age of the concrete. The major influencing factors include:
- Water-Cement Ratio: The water-cement ratio is the single most important factor affecting the modulus of elasticity. Concrete with a lower water-cement ratio will have a higher modulus of elasticity. This is because lower water content leads to lower porosity and higher strength.
- Aggregate Type: Aggregates make up 60-80% of the total volume of concrete. Stiffer aggregates like granite produce concrete with a higher modulus compared to sandstone aggregates.
- Aggregate Volume: Increasing the aggregate volume concentration leads to a higher concrete modulus. The modulus of elasticity of aggregates is generally higher than that of hardened cement paste.
- Cement Type: Concrete made with different types of cements can have varying modulus values. Concrete with pozzolanic materials like fly ash and silica fume tend to have lower modulus than plain Portland cement concrete.
- Age of Concrete: The modulus of elasticity increases over time as the concrete cures and gains strength. Concrete modulus can increase between 30-50% from 7 days to 90 days.
- Compressive Strength: The modulus of elasticity has a close relationship with the compressive strength of concrete. Concrete with higher compressive strength will exhibit higher modulus.
- Curing Conditions: Proper curing is essential for strength and modulus development. Wet curing leads to higher modulus compared to dry curing conditions.
- Loading Rate: The modulus of elasticity varies with the rate of loading. The modulus decreases as the rate of loading increases.

;
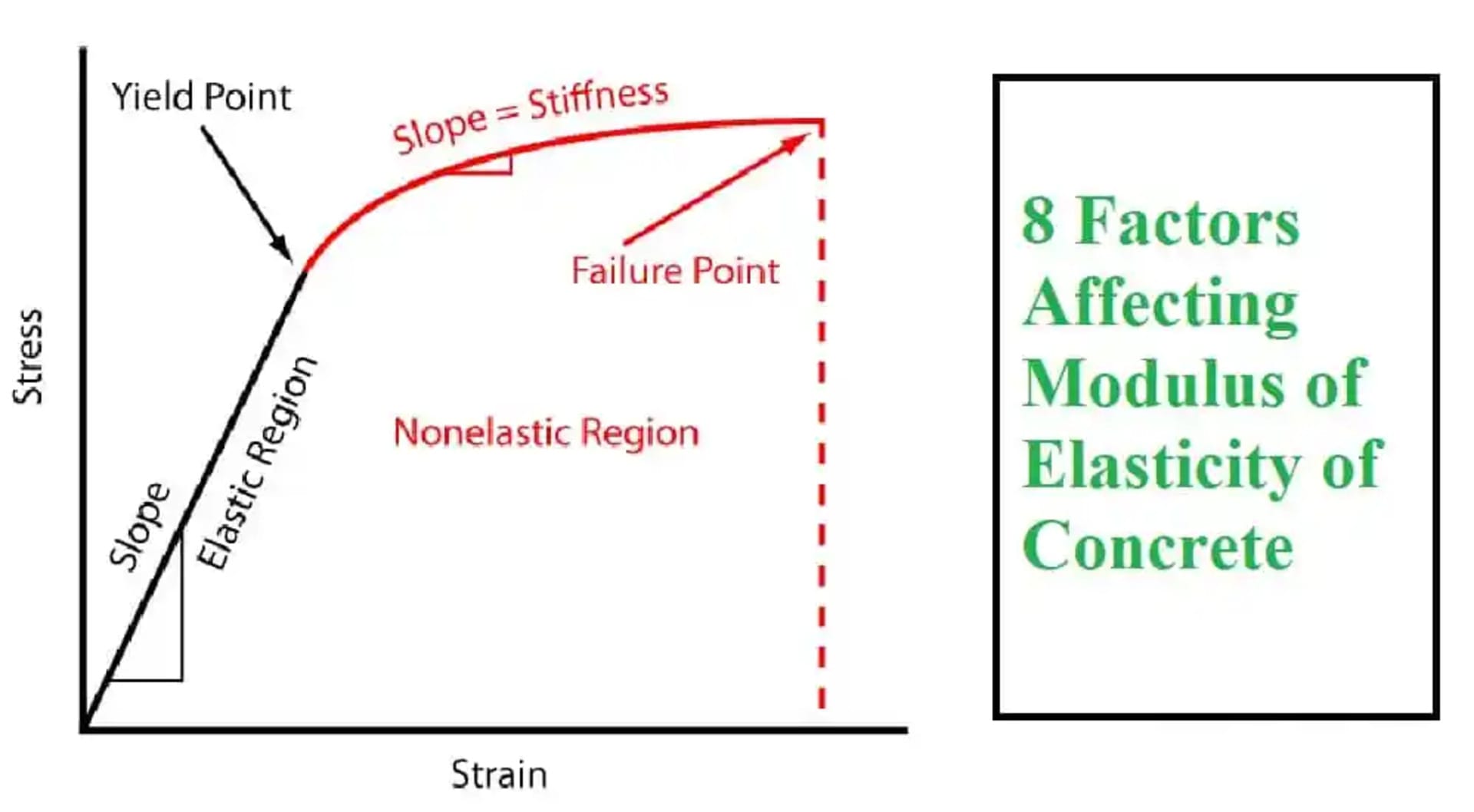
modulus of elasticity curve for concrete
The modulus of elasticity (Ec) of concrete is not a constant value. It varies nonlinearly with the stress applied to the concrete. This stress-strain relationship can be represented by a modulus of elasticity curve.
Key points about the Ec curve for concrete:
- At very low stress levels, the curve is nonlinear and the modulus is low. This is due to closure of existing microcracks.
- As the stress increases, the curve becomes linear. The slope of this portion is the chord modulus of elasticity. This is typically reported as the Ec value.
- The chord modulus represents the elastic range where stress and strain are proportional. The concrete behaves elastically in this region.
- At higher stresses approaching 30-40% of concrete strength, microcracking causes the modulus to decrease. The curve becomes nonlinear again.
- At the maximum stress equal to the compressive strength (f’c), failure occurs and the concrete crushes. Point at this stage on the curve is called yielding point. The corresponding maximum strain is around 0.003.
- The exact shape of the Ec curve depends on concrete strength, curing, type of aggregate, testing procedures and conditions.
- Higher strength concrete will have a higher modulus of elasticity and can sustain more stress before nonlinearity.
- The Ec value used for design and analysis is based on the chord modulus measured in the linear elastic range. This represents the effective stiffness of concrete under working loads.
- Understanding the nonlinear behavior is important for modeling the behavior of concrete structures under overload conditions approaching failure.
In summary, the Ec curve captures the evolving stiffness of concrete under increasing stress and strain. The chord modulus provides the elastic stiffness while the nonlinear regions indicate the progression of internal damage in concrete.
Importance of Modulus of Elasticity in Concrete Design
The modulus of elasticity is a vital parameter in the design of concrete structures. Some of the reasons it is important include:
- Used to compute stresses and deformations in concrete members like beams, columns, and slabs.
- Influences the load-carrying capacity of flexural members. Higher modulus indicates higher stiffness and load resistance.
- Essential for estimating deflections in concrete members subjected to flexural loads.
- Used to estimate crack widths in reinforced concrete sections.
- Helps determine natural frequencies of vibration of concrete structures.
- Allows estimation of prestress losses in prestressed concrete members.
- An input parameter in advanced analysis like finite element modeling of concrete structures.
- Permits calculation of temperature and shrinkage stresses in concrete members.
In summary, the modulus of elasticity is indispensable for safe and optimal concrete structural design. Specifying appropriate modulus values is critical for accurate analysis and modeling.
Modulus of Elasticity Formula
The modulus of elasticity (E) is calculated by dividing the stress (σ) by the strain (ε):
E = σ/ε
For concrete, the modulus is commonly expressed in GigaPascals (GPa) or ksi (1000 psi). Typical values range between 20 to 40 GPa.
Various empirical equations have also been developed to estimate the modulus of elasticity of concrete based on its compressive strength. A simple and widely used formula proposed by ACI 318 is:
Ec = 4700√f’c
Where:
Ec = Modulus of elasticity (MPa)
f’c = Compressive strength of concrete (MPa)
This gives a reasonable approximation of the modulus when the compressive strength is known. However, actual measured values may differ based on concrete mix properties and testing conditions.
Typical Values for Modulus of Elasticity of Concrete
The modulus of elasticity is generally determined by testing concrete cylinders or beams under compression or flexure. Standard test methods include ASTM C469 and ASTM C78. Typical values range from 14 to 41 GPa based on concrete type and strength. Here are some typical values:
- Normal-weight Concrete: 24 to 31 GPa
- Lightweight Concrete: 14 to 17 GPa
- High-strength Concrete: 34 to 41 GPa
- Ultra-high strength Concrete: 42 to 59 GPa
Higher strength concretes like those above 35 MPa tend to have disproportionately higher modulus values. The modulus also varies based on aggregate type. Some typical values are:
- Granite aggregate concrete: 25 to 40 GPa
- Limestone concrete: 21 to 35 GPa
- Sandstone concrete: 14 to 21 GPa
Modulus of Elasticity Values in Design Standards
Different design standards provide prescriptive values and equations to determine the modulus of elasticity for use in analysis and design. Some examples are:
- ACI 318: Provides the formula Ec = 4700√f’c discussed earlier along with minimum Ec values based on strength.
- AS 3600 (Australia): Gives the equation Ec = (ρ1.5 x f’c0.5)/6 with Ec in GPa, ρ is density in kg/m3, f’c is compressive strength in MPa.
- Eurocode 2: Defines the equation Ec = 9500 x [(fck+8)/10]0.3 with fck as the characteristic cylinder strength in MPa.
- IS 456 (India): Defines Ec values of 10, 15 and 25 kN/mm2 for M10, M15, M25 grade concrete respectively.
The suitability of these expressions depends on aggregate type and concrete mixes used. Measured modulus values are recommended for design of major structures.
Modulus of Elasticity of Concrete is Important for Structural Performance
The modulus of elasticity is a key parameter that influences how a concrete structure will perform under various service loads. Using an appropriate value of Ec based on the concrete materials, strength and structural analysis is crucial for:
- Realistic assessment of stress levels and deformations. Lower Ec can lead to excessive deformations.
- Accurate predictions of deflections. Low Ec causes greater flexural deflections.
- Controlling cracking in concrete. Low modulus results in wider crack widths.
- Estimating prestress losses in prestressed concrete. Low Ec leads to higher losses.
- Vibration serviceability. Lower Ec will change natural frequencies.
- Modeling concrete behavior and performance. Inaccurate Ec gives poor correlation.
- Durability against environmental loads. Low modulus concrete is more vulnerable.
By considering the modulus of elasticity and factors that influence it, structural engineers can design more optimal concrete structures. The modulus links material composition to structural performance.
Conclusion
The modulus of elasticity is a vital mechanical property of concrete that determines the load-deformation response and overall structural behavior. It is influenced by the concrete ingredients, mixing, curing conditions and age.
Reliable measurement and use of Ec is crucial for computing stresses, crack control, deflections, and dynamic analysis. Specifying appropriate values based on concrete strength and aggregate type is key for safe and serviceable concrete structure design.