Young’s modulus of steel represents the elastic stiffness property defining deformation resistance in steel.
Correctly leveraging Young’s modulus data enables optimizing civil infrastructure design for safety and serviceability.
This article details calculating, testing and applying this vital mechanical characteristic.
Calculating Young’s Modulus of Steel
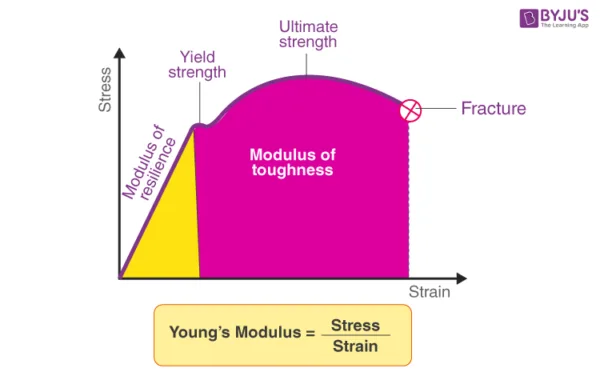
Young’s modulus quantifies steel’s inherent elasticity through the slope of its initial linear stress-strain curve region.
Determining modulus requires a tensile test applying controlled sample loading and measuring extension.
By dividing stress by resulting strain, the proportionality constant derived gives Young’s modulus.
Typical structural steel values range from 190-210 GPa, while high-strength alloys reach 300 GPa.
Definition Young’s Modulus of Steel Explained
Also termed elastic modulus and modulus of elasticity, Young’s modulus represents the mathematical relationship binding experienced stress to resulting elastic strain.
This parameter determines reusable deformability without permanent damage during loading cycles.
Higher modulus values indicate greater stiffness, equivalent to more stress needed to generate a fixed deformation.
Young’s modulus constitutes a fundamental property for modeling steel structural response.
Effect of Composition on Young’s Modulus of Steel
While less composition dependent than strength and ductility, elements like carbon and alloying molybdenum do elevate Young’s modulus values.
Processing via heat treatment and cold working can also boost modulus levels by intensifying crystalline bonding forces resisting dislocation motions.
However, modulus varies less than 10% across common grades.
Minimum expectations rather than maximum limits often dictate design specifications to avoid excessive flexibility.
Role of Young’s Modulus in Steel Design
Young’s modulus features prominently in structural analysis.
For beams, modulus defines flexural stiffness relating bending moments to curvature.
Axial deformation predictions use modulus with cross-sectional area to estimate elongations.
Perhaps most critically, the modulus ratio between steel and concrete enables calculating composite section properties for reinforced members.
Precision modulus data thus improves stress and deflection estimates.
Young’s Modulus Value for Structural Steel
Construction standards provide minimum modulus specifications by grade. For example:
- A36 steel – 200 GPa
- A572 Gr 50 – 205 GPa
- Stainless 304 – 193 GPa
Variations between production heats require testing to determine representative values for critical applications.
Precision measurement empowers realistic modeling.
Relation Between Tensile Strength and Young’s Modulus of Steel
While both metricize mechanical performance, strength and modulus characterize different responses.
Strength indicates load capacity before yielding.
Modulus measures recoverable flexibility without permanent strains.
Their positive correlation results from similar microstructural underpinnings.
But while strength improves dramatically with heat treatment, modulus increases less.
This makes high-strength steels exceptionally rigid.
List of values of Young’s Modulus of Steel Grades
Handbooks tabulate typical steel modulus values:
- Plain carbon steels – 205 GPa
- HSLA and alloy steels – 210 GPa
- Stainless steels – 190-205 GPa
- Tool steels – 210-300 GPa
- Cast steel – 169-205 GPa
Additionally, codes provide grade-specific values.
But custom measurement represents each actual batch definitively.
Testing Methods to Determine Young’s Modulus of Steel
The standard tensile test described above directly measures steel’s modulus. But additional methods also apply:
- Ultrasonic pulse velocity – Wave speed correlates to modulus
- Resonant frequency – Metal vibrations tune to modulus
- Bending tests – Stiffness links to modulus
Still, uniaxial tensile testing remains the definitive quality assurance approach for certifying mechanical properties.
Factors Affecting Steel Young’s Modulus Value
Primarily influenced by:
- Chemistry composition
- Phase proportions
- Production processing history
- Service temperatures
- Specimen geometry details
- Grain sizes and carbide distributions
Integrated computational modeling now predicts combined impacts on achievable modulus.
Young’s Modulus in Elastic Deformation of Steel
Steel relies on elastic modulus for structural resilience. Beams and columns endure cyclic stress fluctuations within proportional limits.
Vibrations, wind buffeting, and seismic events concentrate tremendous cumulative strains over decades, crack initiating without low-cycle fatigue.
Accurately modeling true modulus enables designing flexibility to withstand these demanding repetitive deformations while returning components to precise alignment.
This maintains operational stability and safety margins.
Understanding key roles across steel construction imparts deeper appreciation of Young’s modulus in undergirding structural integrity.
Carefully incorporating accurate property measurements in analysis unlocks superior modeling predictions and optimized material utilization.
This covers interrelated factors affecting, testing and leveraging Young’s modulus data to enhance structural steel performance across the built environment.