Hooke’s law is a principle in physics that states that the force needed to extend or compress a spring is proportional to the extension or compression of the spring from its resting position.
This law has several important applications in engineering, especially civil and mechanical engineering.
This linear relationship between force and displacement holds only when the material deforms elastically up to stresses below its elastic limit.
Beyond this point, permanent deformation and plastic behavior occur instead.
This law has broad relevance across physics, mechanics, engineering, and material science for analyzing elasticity.
Derivation of Hooke’s Law Formula
It can be derived by considering a spring that exerts a restoring force when compressed or extended by a distance x from its equilibrium length.
The restoring force is directly proportional to x, and the constant of proportionality is the spring constant k.
Mathematically, this can be written as:
F = -kx
Where,
F = Restoring force (N)
k = Spring constant (N/m)
x = Extension or compression distance (m)
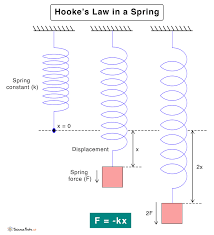
The negative sign indicates that the restoring force always acts in the opposite direction of the displacement.
This is the mathematical expression of Hooke’s law.
Examples with Solutions
Example 1: A spring has a spring constant of 100 N/m. How much force is required to stretch it by 0.05 m?
Solution:
Given: k = 100 N/m x = 0.05 m
F = ?
Substitute the values in Hooke’s law:
F = – kx
= – (100 N/m)(0.05 m)
= – 5 N
Therefore, a force of 5 N is required to stretch the spring by 0.05 m.
Limitations
While this law is valid for most real-world springs, it does have certain limitations:
- It is only valid for small deformations of the spring, up to a few percent.
- Permanently deforms spring if force exceeds elastic limit.
- Not valid for nonlinear springs or deformation in plastic region.
- Ignores stress concentrations and material defects.
- Assumes uniform deformation across spring wire/material.
So when these assumptions break down or the material deforms plastically, this law will no longer apply accurately.
Difference Between Hooke’s Law and Spring Constant
- This law describes relationship between force and deformation of spring.
- Spring constant is the proportionality constant in this relationship.
- So it focuses on overall force-displacement behavior, while spring constant is a specific property of the spring measuring stiffness.
Applications in Engineering
It has many uses in mechanical and civil engineering applications:
- Designing springs and suspension: Formula used to customize spring stiffness for application by choosing material and dimensions.
- Sensors and measurement devices: Load cells, weighing scales, MEMS devices use spring deformation to measure force in relative displacement sensors.
- Material testing: Tensile tests apply Hooke’s law to measure Young’s modulus from stress-strain curve in elastic region.
- Earthquake engineering: Mathematical models of buildings use Hooke’s law springs to simulate response of structures to seismic vibrations.
- Fatigue analysis: Repeated deformation below elastic limit causes material failure over time, and Hooke’s law informs estimation of device lifespans.
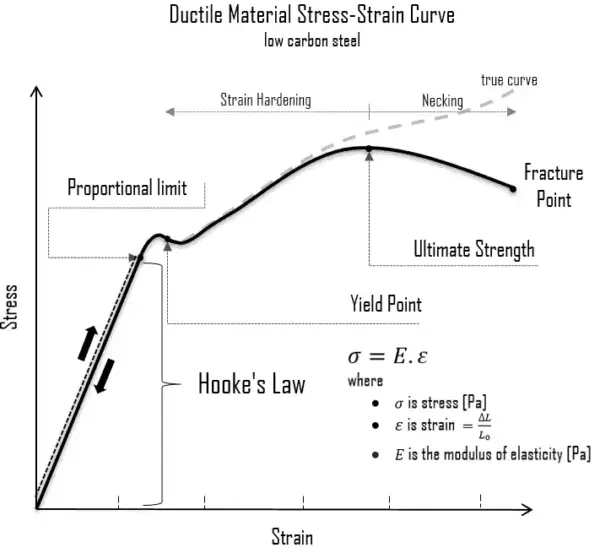
Stress vs Strain Hooke’s Law Graph
Hooke’s law can also be expressed in terms of stress and strain. In this form, the law states that stress is proportional to strain in the elastic region:
σ = Eε
Where,
σ = Stress (Pa)
E = Young’s modulus (Pa)
ε = Strain (dimensionless)
This relationship is linear up to the elastic limit, just like the force-displacement graph.
Hooke’s Law for Tensile Stress and Strain
For a material under tensile loading, Hooke’s law in stress-strain form can be applied within elastic limits:
σ = (F/A) = (E)(ΔL/L)
Where,
F = Applied axial force
A = Cross-sectional area
L = Original length
ΔL = Change in length
This form is useful for tensile testing to compute unknowns like Modulus of Elasticity (E).
Uses of Hooke’s Law in Physics
In physics, Hooke’s law serves following purposes:
- Analyzing oscillatory motion of springs and pendulums
- Studying elastic potential energy stored in spring due to deformation
- Understanding restoring forces acting on displaced objects
- Modeling behavior of oscillators in wave theory and simple harmonic motion
- Describing force interactions between atoms and molecules at microscopic scales
Overall, it forms basis for studying many oscillatory systems across macro and micro scales in physics.
Conclusion
In conclusion, Hooke’s law provides the foundation for quantitatively understanding elastic deformation across strain levels, forces, material properties, and spring dynamics.
Hooke’s law is critical for civil engineers across mechanical design, material testing, earthquake engineering, and other domains.
Hooke’s ubiquity across diverse fields like physics, mechanical engineering, and material science underscores its lasting impact through the centuries as a keystone theory of elasticity.
Harnessing this law while navigating its boundaries drives innovation.